Distributional and frequency effects in word embeddings

© 2018 Chris Culy, June 2018, rev. 2 July 2018

chrisculy.net

Summary

Word embeddings/vectors are meant to encode meaning without regard to the frequencies of the words BUT in practice the word frequencies have an effect on the vectors and more importantly on their similarities.

This matters since word vectors are used as input to other models — if the word vectors are distorted that could have a negative effect on the downstream components.

In this series of posts, I will look at a range of distributional and frequency effects in word embeddings, many of which are presented here for the first time. I consider four different models (Skip-Gram with Negative Sampling (sgns), FastText (ft), Glove, and Positive pointwise mutual information (ppmi) and show how they are similar and where they are different. The fact that they have different properties strongly suggests that the effects are not due to properties of language, but properties of the models.

In a subsequent series, I will set out a framework for exploring mitigating strategies, strategies whose goal is to improve performance on some metric, and show how those strategies perform on a couple metrics, including word similarities.

TL;DR: Results and Contributions

High level only. More details in the sections

  • Frequency effects are pervasive
  • The effects differ for different embedding methods
    • sgns and ft often pattern together, as do glove and ppmi
  • The effects differ across corpora
    • sgns and ft do not discriminate well for very small corpora
  • Shifted similarity distributions
    • The distributions of word similarities have a positive mean
    • Random vectors are effectively not skewed
    • Corpus size may affect distributions, but not always
  • Similarity stratification
    • Similarity is related to the frequencies of the words being compared
    • Rank is related to the frequencies of the words being compared
    • "Reciprocity" is related to the frequencies of the words being compared
  • Frequency effects of vectors
    • Vectors encode frequency information but very little for very low frequency words
    • Individual dimensions encode relatively little information about frequency
    • The "power law" for nearest neighbors [1] is mostly not reproduced with these methods and these small corpora
  • Strange geometry
    • The two distributional phenomena from [2] hold up pretty well across the methods and with small corpora.
  • Distributional effects and hubs
    • Word embeddings usually have hubs, but limited with very small corpora
    • Hubs vary by method
    • Hubs show frequency effects
    • Stratification of similarities is not sufficient to explain the hub frequency effects

Introduction

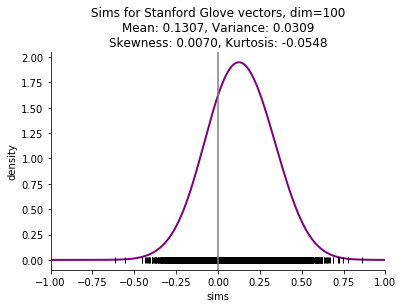
My point of departure is the observation that distribution of word similarities in a corpus does not span the full range that is theoretically possible, and it is skewed. Introductory discussions of word embeddings talk about using the cosine of the angle between two vectors as the most common measure of similarity, and that the cosine ranges from -1 to 1. While that is mathematically correct, the observed cosine similarities in a corpus may not range from -1 to 1. Furthermore, the mean of the distribution is positive, not 0 as we might expect. Here is an example, using the Stanford Glove vectors, which are derived from Wikipedia and Gigaword. This shows the density estimate of the distrbution (the curved line) and the similarities that were sampled uniformly from all the similarities (the small vertical lines along the x axis).

Histogram of Stanford Glove vectors, 100 dimensions

I am particularly interested in small corpora, such as a single book, and the skew is even more striking with these small corpora. Here are examples comparing the four embedding methods mentioned above (skip n-gram with negative sampling (sgns), FastText (ft), Glove, and pointwise mutual information with svd (ppmi)) on Thackeray's Vanity Fair.

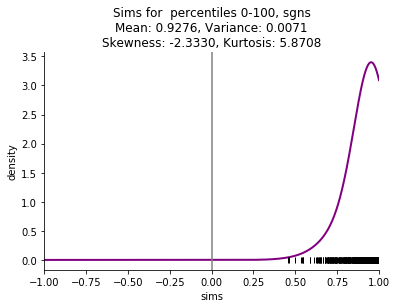
Histogram of SGNS vectors for Vanity Fair, 100 dimensions

Histogram of FastText vectors for Vanity Fair, 100 dimensions

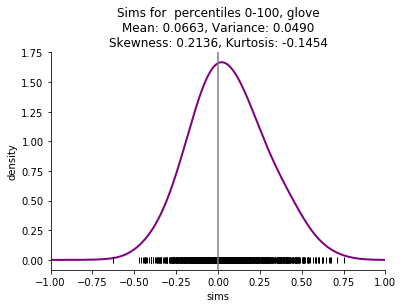
Histogram of Glove vectors for Vanity Fair, 100 dimensions

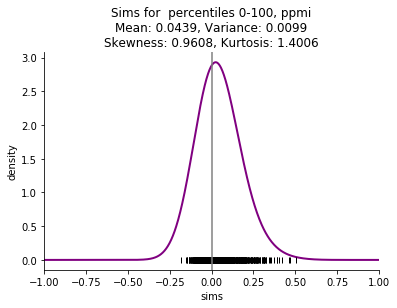
Histogram of PPMI vectors for Vanity Fair, 100 dimensions

This starting point of shifted distributions will lead to a series of other related phenomena:

  • stratification effects of similarties: similarities are not independent of the frequencies in the corpus of the words being compared
  • vectors encode some information about word frequency in the corpus
  • vector spaces have "hubs": some words are very similar to many words,
    • those hubs are not independent of the frequency of the words, hubs and non-hubs

In each case I will compare the 4 models (as above) and point out similarities and differences across them. The differences show that the phenomena are not intrinsic to the corpus the vectors are derived from, but rather connected to the models. More generally, we want to know which (parts of) the phenomena are due to the nature of vector spaces (e.g. hubs), which are due to the particulars of the models (e.g. direction of stratification correlation), and which are due to the nature of language (e.g. perhaps the existence of frequency effects).

Although the distribution of vectors is distorted, it could be the case that these distortions are not a problem, or even that they are a positive factor. In a subsequent series, I will propose a conceptual framework for exploring how we can address the issues of distortion, and then show that these techniques can have a positive effect for some intrinsic evaluation, including word similarities.

In a nutshell, the conceptual framework is simply the observation that we can make 3 different kinds of modifications to our models (broadly construed):

  1. We can modify the vectors themselves
  2. We can change the similarity measure from the simple cosine similarity
  3. We can adjust the calculated similarities post hoc

Of course, we can also do all of those in combination.

Finally, in addition to the types of modification techniques, some methodological recommendations arise from this work, namely:

  • Pretrained vectors should include the frequency information of the items
  • Given that corpus sizes vary tremendously, investigations should be done using relative frequencies rather than absolute frequencies or "top N"

Technical details

Preprocessing

For simplicity, I'll use a very simple preprocessing step, slightly elaborated from the hyperwords package [3]. The preprocessing converts the input to ascii, lowercases it, and removes punctuation except for the apostrophes of contractions and possessive 's. Tokens are words, contractions (except n't is not a separate token), and the possessive 's. The actual command is the following:

iconv -c -f utf-8 -t ascii $1 | tr '[A-Z]' '[a-z]' | sed -E "s/[^a-z0-9']+/ /g" | sed -E "s/ '/ /g" | sed -E "s/' / /g" | sed -E "s/^'//g" | sed -E "s/'$//g" | sed -E "s/'v/ 'v/g" | sed -E "s/'ll/ 'll/g" | sed -E "s/'s/ 's/g" | sed -E "s/'d/ 'd/g" | sed -E "s/i'm/i 'm/g" | sed -E "s/'re/ 're/g" | sed -E "s/  +/ /g"

I have used spacy to split the input into sentences before doing the preprocessing.

Word vector calculations

In calculating the word vectors, I have used the genim [3] implementations of Skip Gram with Negative Sampling (sgns) and FastText. For Glove vectors, I use the original implementation [4]. For PPMI with SVD I use the hyperwords package [5] implementation, ported by me to Python3.

Acknowledgment

Thanks to John Bear for helpful suggestions. All faults are mine.

Individual postings

References

[1] Tobias Schnabel, Igor Labutov, David Mimno, and Thorsten Joachims. 2015. Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing.

[2] David Mimno and Laure Thompson. 2017. The strange geometry of skip-gram with negative sampling. Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, 2873–2878.

[3] Gensim: https://radimrehurek.com/gensim/, published as "Software Framework for Topic Modelling with Large Corpora" Radim Řehůřek and Petr Sojka, Proceedings of the LREC 2010 Workshop on New Challenges for NLP Frameworks, pp. 45-50.

[4] Glove: https://nlp.stanford.edu/projects/glove/, pubished as "GloVe: Global Vectors for Word Representation" Jeffrey Pennington, Richard Socher, and Christopher D. Manning. Empirical Methods in Natural Language Processing (EMNLP) 2014. pp. 1532--1543

[5] Hyperwords: https://bitbucket.org/omerlevy/hyperwords, published as "Improving Distributional Similarity with Lessons Learned from Word Embeddings" Omer Levy, Yoav Goldberg, and Ido Dagan. TACL 2015.

In [ ]: